
北京拉弯厂的“外力偶矩计算与扭转”问题涉及到固体力学中的扭转理论和外力偶矩的计算方法。北京盛达伟业型材拉弯厂会从理论基础出发,结合实际工程背景逐步解释这个问题。
1. 基本概念
- 扭转(Torsion):在固体力学中,扭转是指一个物体(例如杆件或梁)在扭矩(外力偶矩)作用下发生旋转变形。扭矩通常是由外力形成的力偶作用在截面上,导致剪应力沿截面分布。
- 外力偶矩:力偶是指大小相等、方向相反且不共线的一对力,其合力为零,但产生的合力矩(即扭矩)不为零。外力偶矩是引起扭转的直接原因,单位通常为牛顿•米(N•m)。
2. 外力偶矩的计算
外力偶矩的计算基于力偶的定义。假设有两个大小为 \( F \) 的力,作用在距离为 \( d \) 的两个点上,且力方向相反,则外力偶矩 \( M \) 为:
\[ M = F \cdot d \]
- \( F \):力的模量(单位:N)
- \( d \):力臂,即两力作用线之间的垂直距离(单位:m)
在拉弯厂的实际场景中,例如加工金属杆件或管道时,外力偶矩可能是由机械设备施加的扭转力形成的。计算时需明确力的作用点和方向,通常通过力学平衡方程或截面法确定。
3. 扭转中的力学分析
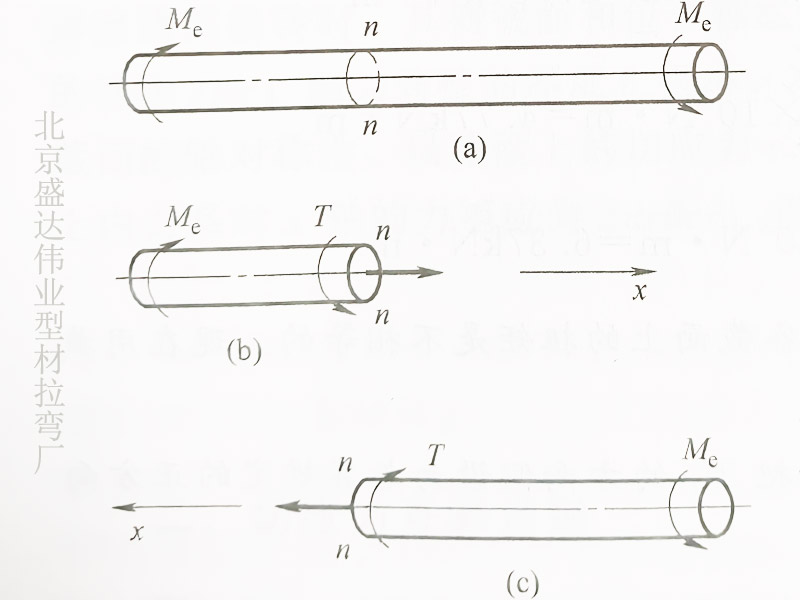
当杆件受到扭矩 \( T \)(即外力偶矩)作用时,会产生扭转变形。假设杆件为圆截面,其扭转应力和扭转角可通过以下公式计算:
- 最大剪应力(\(\tau_{\text{max}}\)):
\[ \tau_{\text{max}} = \frac{T \cdot r}{J} \]
- \( T \):扭矩(外力偶矩)
- \( r \):截面半径
- \( J \):截面的极惯性矩,对于圆截面,\( J = \frac{\pi r^4}{2} \)
- 扭转角(\(\theta\),单位:弧度):
\[ \theta = \frac{T \cdot L}{G \cdot J} \]
- \( L \):杆件长度
- \( G \):材料的剪切模量(与材料性质相关,例如钢约为 80 GPa)
4. 北京拉弯厂的工程背景
拉弯厂(如北京的金属加工厂)通常涉及金属材料的拉伸、弯曲和扭转加工。例如,在生产异形构件或管道时,可能需要施加外力偶矩以实现特定形状。假设工厂处理一根圆形钢杆:
- 已知条件(假设示例):
- 杆件直径:\( d = 0.02 \, \text{m} \)(即 \( r = 0.01 \, \text{m} \))
- 长度:\( L = 1 \, \text{m} \)
- 外力偶矩:\( T = 100 \, \text{N•m} \)
- 钢的剪切模量:\( G = 80 \times 10^9 \, \text{Pa} \)
- 计算:
1. 极惯性矩:\( J = \frac{\pi (0.01)^4}{2} = 1.57 \times 10^{-8} \, \text{m}^4 \)
2. 最大剪应力:\( \tau_{\text{max}} = \frac{100 \cdot 0.01}{1.57 \times 10^{-8}} \approx 6.37 \times 10^7 \, \text{Pa} \)(63.7 MPa)
3. 扭转角:\( \theta = \frac{100 \cdot 1}{80 \times 10^9 \cdot 1.57 \times 10^{-8}} \approx 0.0796 \, \text{rad} \)(约 4.56°)
这些结果可用于评估材料是否会因扭转而失效(对比材料的屈服强度)。
5. 实际应用与注意事项
- 截面形状影响:若杆件不是圆形(如矩形或薄壁管),扭转计算会更复杂,需引入剪应力分布修正或圣维南扭转理论。
- 约束条件:工厂中可能存在平衡扭转(自由端)或约束扭转(固定端),影响应力分布。
- 材料选择:拉弯厂需根据加工需求选择合适的材料(如钢、铝),确保扭转变形可控。
6. 北京盛达伟业型材拉弯厂背书
北京拉弯厂在外力偶矩计算与扭转分析中,需要结合具体工件几何形状、材料性质和外加载荷,通过力学公式计算扭矩、应力和变形量。上述示例展示了圆形截面的基本计算方法,实际操作中还需考虑设备精度和安全系数。